Interactive Session 2A

Derivatives by hand, in R, meet git & GitHub

1. Derivatives by hand

Find the first derivative of the following functions the long way

Use the definition of the derivative:

\[\frac{df}{dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]

  1. \(f(x)=3x^2-x+1\)

\(f(x)=3x^2-x+1\)

\(=\lim_{h\to 0}\frac{3(x+h)^2-(x+h)+1-(3x^2-x+1)}{h}\)

\(=\lim_{h\to 0}\frac{3(x^2+2xh+h^2)-x-h+1-3x^2+x-1)}{h}\)

\(=\lim_{h\to 0}\frac{3x^2+6xh+3h^2-x-h+1-3x^2+x-1)}{h}\)

\(=\lim_{h\to 0}\frac{3h^2+6xh-1}{h}\)

\(=\lim_{h\to 0}3h+6x-1\)

\(=6x-1\)

  1. \(G(t)=4-3t\)

\(G(t)=4-3t\)

\(=\lim_{h\to 0}\frac{4-3(t+h)-(4-3t)}{h}\)

\(=-3\)

Find the first derivative of the following using rules

  1. \(f(x) = -3x^5+2x^3-12\)

\(f(x) = -3x^5+2x^3-12\)

\(\frac{df}{dx} = -(3)(5)x^4+(2)(3)x^2-0\)

\(\frac{df}{dx} = -15x^4+6x^2\)

  1. \(C(z)=4.2z-8.7z^3\)

\(\frac{dC}{dz} = 4.2 - (3)(8.7)z^2\)

\(\frac{dC}{dz} = -26.1z^2 + 4.2\)

Find an instantaneous slope

  1. A researcher finds that the increase in algal biomass (\(B\), in grams) in their aquarium over time (\(t\), in hours) follows the function:

\[B(t) = 0.4 + 0.035t^2\]

  • What is the mass of algae in tank at 4.5 hours?

\(B(t) = 0.4 + 0.035t^2\)

\(B(4.5) = 0.4 + 0.035(4.5)^2\)

\(B(4.5) = 0.4 + 0.035(20.25)\)

\(B(4.5) = 0.4 + 0.70875\)

\(B(4.5) = 1.10875 \ grams\)

  • At what rate is biomass increasing in the tank after 10 hours?

\(B(t) = 0.4 + 0.035t^2\)

\(\frac{dB}{dt} = 0 + (0.035)(2)t\)

\(\frac{dB}{dt} = 0 + (0.035)(2)(10)\)

\(\frac{dB}{dt} = 0.7 \ grams/hr\)

2. Derivatives in R with D()

  1. Create a new R project named eds212-day2a
  2. To the project, add an R script (discuss how a script differs from a Quarto doc)
  3. Add a header (comment out lines with # in a script)
  4. Follow along to find the derivative of several functions using D() (and optionally, deriv())

Just because we aren’t working in a Quarto document (where we can combine prose and code) doesn’t mean clear annotations and section headers aren’t important!

The {ARTofR} package is wonderful for creating clean titles, dividers, and block comments for your code. Install the RStudio Addin, or call {ARTofR} functions in your console to generate comments, copy to your clipboard, and paste into your scripts.

If you opt for the function / console approach:

  1. Load the package (library(ARTofR)) in your Console (rather than in your script/qmd file)
  2. Select the function for your preferred divider (see the package README for options, or type xxx_ into your Console, which should pull up an auto fill list of options)
  3. Type that function, along with your section header text (e.g. xxx_title2("My section title")) into the console – the resulting divider is automatically copied to your clipboard
  4. Paste your divider into your script

For example:

xxx_title2("text here")

creates the header:

##~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
##                                  text here                               ----
##~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

And:

xxx_divider1("text here")

creates the divider:

#............................text here...........................

There are two functions, D() and deriv(), which can be used to compute the derivatives of expressions in R. Both accept two arguments, expr (an expression or formula) and name (the variable that the derivative will be carried out with respect to). We’ll focus primarily on using D(), but examples are provided for using deriv() as well:

Using D():

D() computes the derivative of a simple expression. Let’s use D() to evaluate the same expression, \(5x^2\), again at \(x = 2.8\):

# Create an expression (right hand side of the equation) ----
my_expression <- expression(5 * x^2)

# Find the derivative of your expression with respect to x using `D()` ----
my_derivative <- D(expr = my_expression, name = "x")

# Check it out ----
my_derivative
5 * (2 * x)
# Evaluate it at x = 2.8 ----
x <- 2.8

# Evaluate it! (value returned is slope) ----
eval(my_derivative)
[1] 28

Using deriv():

Using deriv() is valuable when you encounter more complex scenarios where you need to evaluate both the function and it’s derivative(s). It can handle multivariate functions, and is useful in optimization contexts (so you may see this again in machine learning!). The code looks pretty similar to the example using D(), above, but it returns a bit more information in the output:

# Create an expression (right hand side of the equation) ----
my_expression <- expression(5 * x^2)

# Find the derivative of your expression with respect to x using `deriv()` ----
my_derivative <- deriv(expr = my_expression, name = "x")

# Check it out ----
my_derivative
expression({
    .value <- 5 * x^2
    .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
    .grad[, "x"] <- 5 * (2 * x)
    attr(.value, "gradient") <- .grad
    .value
})

There’s a lot going on in the above output, but what’s important to take away is that our expression returns the original function (\(5 \times x^2\); see the line, .value <- 5 * x^2) and it’s derivative (\(5 \times (2 \times x)\); see the line, .grad[, "x"] <- 5 * (2 * x)). This means, when we evaluate our expression at a particular value of x, it will return both the value of the function at \(x\) and the value of the derivative (slope) at \(x\). Let’s do that now:

# Let's say we want to evaluate our derivative at x = 2.8 ----
x <- 2.8

# Evaluate it! (first returned is function value, second returned is slope) ----
eval(my_derivative)
[1] 39.2
attr(,"gradient")
      x
[1,] 28

The above code evaluates both our original function and it’s derivative at \(x = 2.8\):

  • Evaluate our original function at \(x = 2.8\)
    • \(5 \times 2.8^2 = 39.2\)
  • Evaluate the derivative at \(x = 2.8\)
    • \(5 \times (2 \times 2.8) = 28\)

3. More examples with D()

Example 1:

You don’t have to save your expression as it’s own variable (though it is good practice to break things into smaller, easy-to-read pieces, when possible) – we can write our expression directly inside D() where the first expr argument is expected:

# Find the derivative with respect to x ----
my_derivative <- D(expr = expression(3.1 * x^4 - 28 * x), name = "x")

# Check it out ----
my_derivative
3.1 * (4 * x^3) - 28

Example 2:

# Create and store your function ----
fx <- expression(x^2)

# Find the derivative with respect to x (using `D()` function) ----
df_dx <- D(expr = fx, name = "x")

# Return the derivative ----
df_dx
2 * x
# Find the slope at x = 10 ----
x <- 10
eval(df_dx)
[1] 20

You try!

Using the D() function in R:

  1. Find \(\frac{dg}{dz}\) given: \(g(z) = 2z^3-10.5z^2+4.1\)
  2. Find \(\frac{dT}{dy}\) given: \(T(y) = (2y^3+1)^4-8y^3\)
  1. \(g(z) = 2z^3-10.5z^2+4.1\)
gz = expression(2*z^3 - 10.5*z^2 + 4.1)
dg_dz = D(expr = gz, name = "z")
  
# Return dg_dz ----
dg_dz
2 * (3 * z^2) - 10.5 * (2 * z)
  1. \(T(y) = (2y^3+1)^4-8y^3\)
ty = expression((2*y^3+1)^4 - 8*y^3)
dt_dy = D(expr = ty, name = "y")
  
# Return dt_dy ----
dt_dy
4 * (2 * (3 * y^2) * (2 * y^3 + 1)^3) - 8 * (3 * y^2)

To find the slope of T(y) at a range of y-values:

We found \(\frac{dT}{dy}\) above. What if we want to find the slope at a range of values, instead of just one?

# Create a vector of y values from -0.4 to 2.0, by increments of 0.1 ----
y <- seq(from = -0.4, to = 2.0, by = 0.1)

# Evaluate the slope of T(y) at each of those values ----
eval(dt_dy)
 [1] -1.293869e+00 -3.313644e-01 -4.534665e-02 -1.437122e-03  0.000000e+00
 [6]  1.442882e-03  4.682121e-02  3.691558e-01  1.671357e+00  5.718750e+00
[11]  1.673130e+01  4.460117e+01  1.119970e+02  2.692568e+02  6.240000e+02
[16]  1.397065e+03  3.023241e+03  6.324914e+03  1.279990e+04  2.508216e+04
[21]  4.765645e+04  8.793682e+04  1.578538e+05  2.761395e+05  4.715520e+05

4. Hello git & GitHub

Enter hand waving & storytelling: Why git & GitHub (Horst & Lowndes)

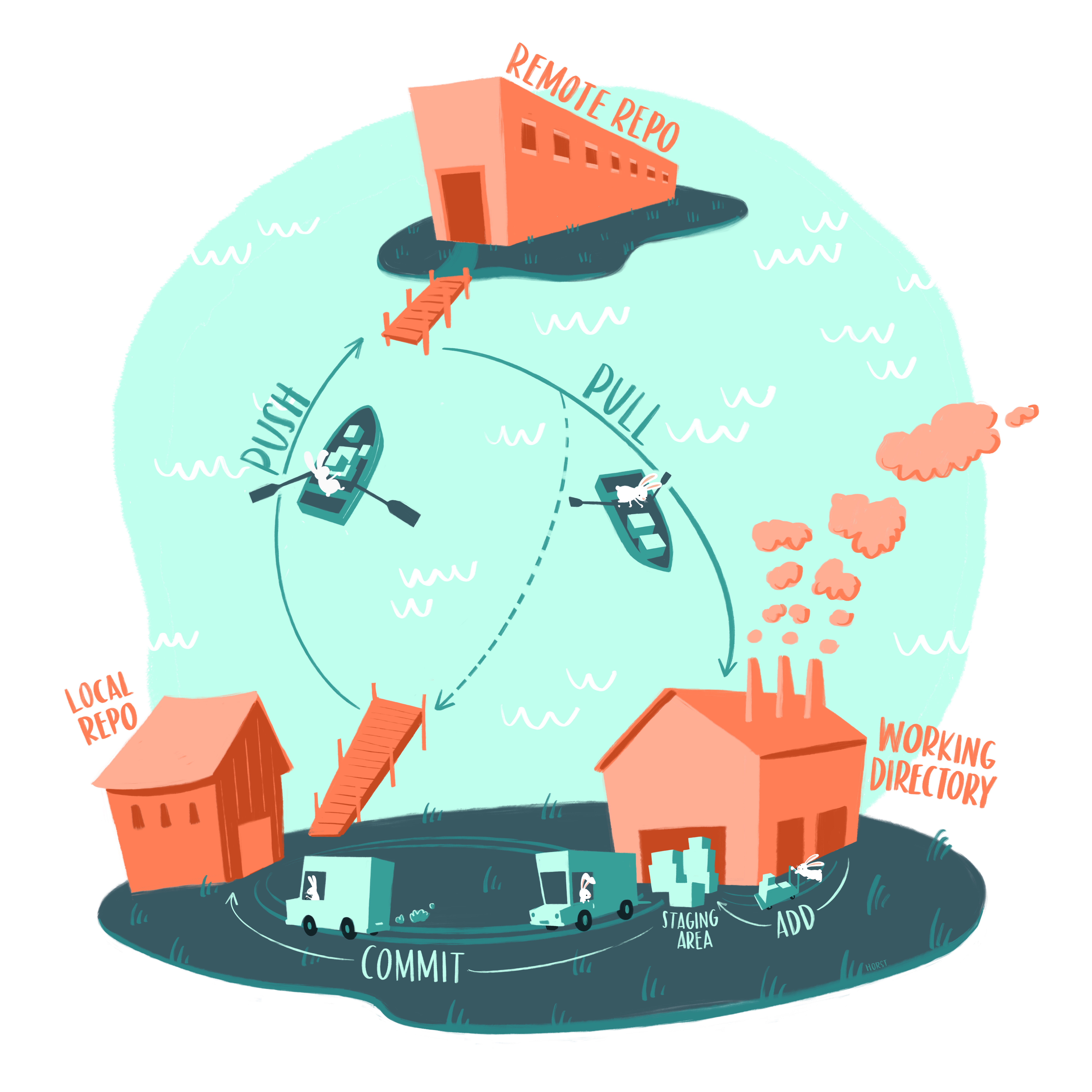
Schematic of basic git solo user workflow. Artwork by Allison Horst

Getting started

1. Make a new R Project

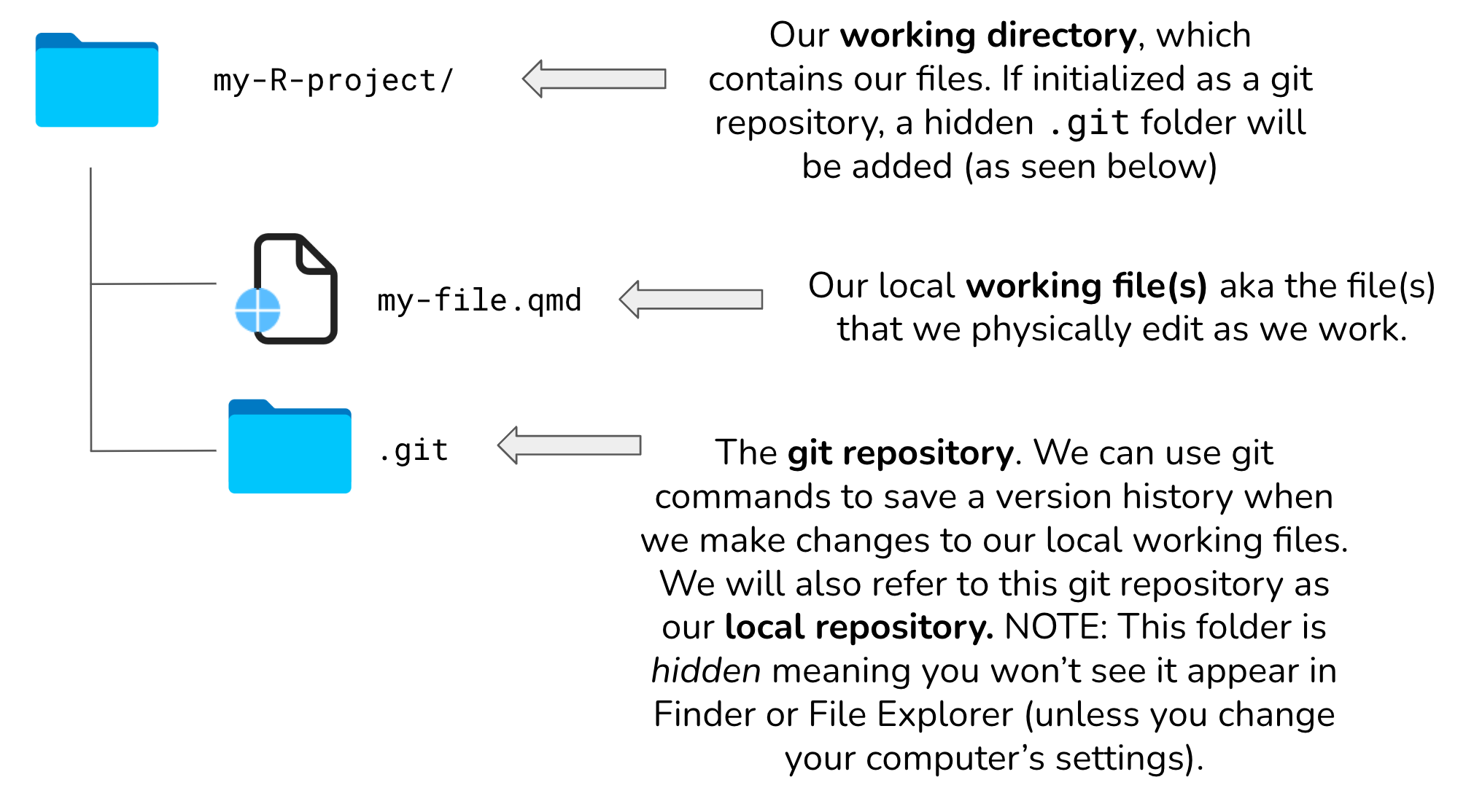
  • Create a new R Project and name it eds212-day2-GHpractice
  • Add a new Quarto document
  • Render (it’ll prompt you to name / save the file first; I’ll name mine day2a-vc-gh.qmd)

2. Add version control w/ git

  • In the Console, run usethis::use_git() (press Enter, then enter the number for YES when prompted)
  • This makes your local git repo

When we initialize our R project as a git repository using usethis::use_git(), a hidden git/ folder is created within that project folder. This hidden .git/ folder is the git repository. As you use git commands (or RStudio’s GUI buttons) to capture versions or “snapshots” of your work, those versions are stored within the .git/ folder. This allows you to access and / or recover any previous versions of your work. If you delete .git/, you delete your project’s history.

3. Connect to remote repo

  • In the Console, run usethis::use_github() (press Enter, then enter the number for YES when prompted)
  • This has connected your local git repo to the remote repo (on GitHub), and pushed updates automatically

4. Make, stage, commit & push some changes

  • In your .qmd, make some changes (whatever you want). Save. Render (or not…as long as one file changes).
  • Notice that in the git tab in RStudio, the file(s) you updated show up as having been updated.
  • Stage (check box next to files), Commit (add commit message), Pull (for habit to check for remote changes), then Push to the remote repo. Go to your remote repo on GitHub, refresh page, and see your latest commit message + updates!

5. A bit more ggplot fun

Let’s customize a graph a little bit. Here, we’ll use the penguins dataset from the {palmerpenguins} package.

Some extras we’ll learn here are:

  • Adding axis labels, titles & subtitles
  • A few new graph types
  • Faceting
  • Updating colors
# load libraries ----
library(tidyverse)
library(palmerpenguins)

# create plot ----
ggplot(data = penguins, aes(x = body_mass_g, y = flipper_length_mm)) +
  geom_point(aes(color = species)) +
  scale_color_manual(values = c("darkorange","purple","cyan4")) +
  labs(x = "Body mass (g)",
       y = "Flipper length (mm)",
       title = "Palmer penguin size measurements",
       subtitle = "Palmer Archipelago, Antarctice (2007 - 2009)",
       caption = "Collected by Dr. Kristen Gorman and colleagues at Palmer Station LTER") +
  facet_wrap(~island) +
  theme_minimal()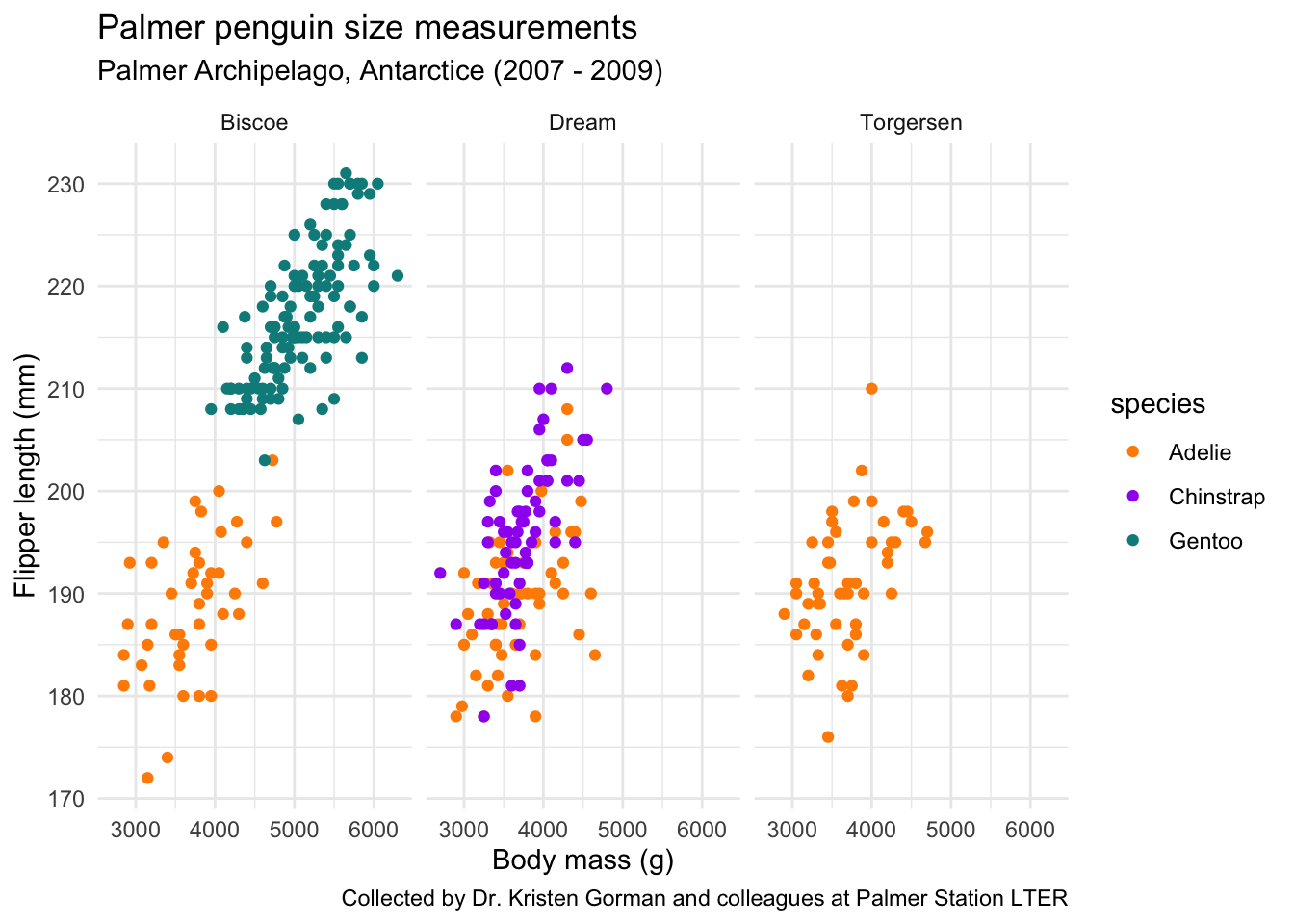

  • Stage, commit, pull, push.


End interactive session 2A