Interactive Session 4A

Linear algebra continued: matrices in R and a Leslie Matrix example

1. Set up

  1. Create a new repository on GitHub called eds212-day4a, with a README
  2. Clone and create a new version-controlled R Project
  3. Add a new Quarto document, save as r-matrices.qmd

2. Matrices

A matrix contains data of a single class (usually numbers). Which means that we can think of the contents of a matrix as a single sequence of values, that are constrained (wrapped) to the specified dimensions of the matrix.

For example, let’s say we have 10 values:

# Make a sequence of values from 1 - 10 ----
my_values <- seq(from = 1, to = 10, by = 1)

# Look at it (always) ----
my_values
 [1]  1  2  3  4  5  6  7  8  9 10

Now, we can convert this into a matrix by letting R know how many rows these values should be “wrapped” into (the default is to populate by column…see documentation, and always look at what you’ve created):

# Convert to matrix ----
my_matrix <- matrix(data = my_values, nrow = 2, ncol = 5, byrow = TRUE)

# Check it out ----
my_matrix
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    6    7    8    9   10

Try some other variations to make a matrix from my_values to test it out. What happens if you don’t have enough elements in the matrix to contain your vector?

For example:

matrix(data = my_values, nrow = 2, ncol = 3, byrow = TRUE)
Warning in matrix(data = my_values, nrow = 2, ncol = 3, byrow = TRUE): data
length [10] is not a sub-multiple or multiple of the number of columns [3]
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6

What happens if your matrix has more elements than your vector?

For example:

matrix(data = my_values, nrow = 3, ncol = 4, byrow = TRUE)
Warning in matrix(data = my_values, nrow = 3, ncol = 4, byrow = TRUE): data
length [10] is not a sub-multiple or multiple of the number of rows [3]
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10    1    2

So…always, always, always look at what you’ve created.

Scalar multiplication, addition and subtraction

Scalar multiplication of a matrix is straightforward: just use the multiply operator (*):

4 * my_matrix
     [,1] [,2] [,3] [,4] [,5]
[1,]    4    8   12   16   20
[2,]   24   28   32   36   40

Addition/subtraction requires matrices of the same dimension. Let’s make another 2x5 matrix:

# Make 2x5 matrix ----
my_values2 <- seq(from = 21, to = 30)
my_matrix2 <- matrix(my_values2, nrow = 2, byrow = TRUE)

# Check it out ----
my_matrix2
     [,1] [,2] [,3] [,4] [,5]
[1,]   21   22   23   24   25
[2,]   26   27   28   29   30

Add the two matrices:

my_matrix + my_matrix2
     [,1] [,2] [,3] [,4] [,5]
[1,]   22   24   26   28   30
[2,]   32   34   36   38   40

Similarly for subtraction:

my_matrix2 - my_matrix
     [,1] [,2] [,3] [,4] [,5]
[1,]   20   20   20   20   20
[2,]   20   20   20   20   20

Matrix multiplication

As we saw in lecture, matrix multiplication is a bit more complicated (dot products of rows by columns become elements in the resulting matrix). Here’s a reminder:

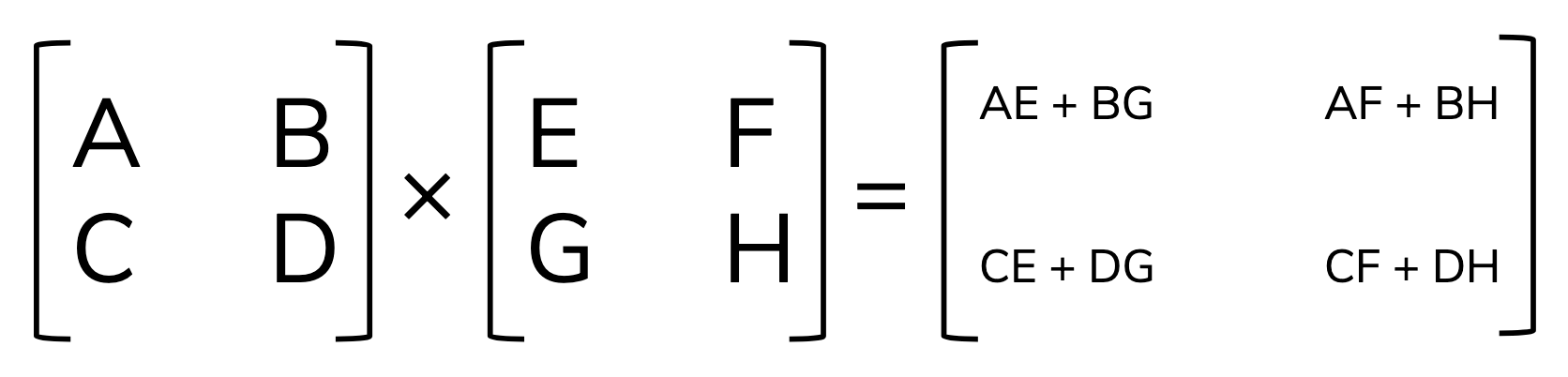
We multiply matrices in R using the same operator as the dot product for vectors: %*%

For example:

# Make a couple of 2x2 matrices ----
cats <- matrix(data = c(0,4,3,1), nrow = 2, byrow = TRUE)
dogs <- matrix(data = c(6,-3,0,2), nrow = 2, byrow = TRUE)

# Look at them ----
cats
     [,1] [,2]
[1,]    0    4
[2,]    3    1
dogs
     [,1] [,2]
[1,]    6   -3
[2,]    0    2
# Matrix multiplication ----
cats %*% dogs
     [,1] [,2]
[1,]    0    8
[2,]   18   -7

Confirm that this is correct by doing the matrix multiplication by hand.

3. A Leslie Matrix example

In lecture, we considered a Leslie matrix for an insect with three life stages, that looked like this:

Create the projection matrix:

# Create your matrix ----
insect_leslie <- matrix(c(0, 0, 600, 0.2, 0, 0, 0, 0.08, 0), nrow = 3, ncol = 3, byrow = TRUE)

# Check it out ----
insect_leslie
     [,1] [,2] [,3]
[1,]  0.0 0.00  600
[2,]  0.2 0.00    0
[3,]  0.0 0.08    0

Specify an initial condition

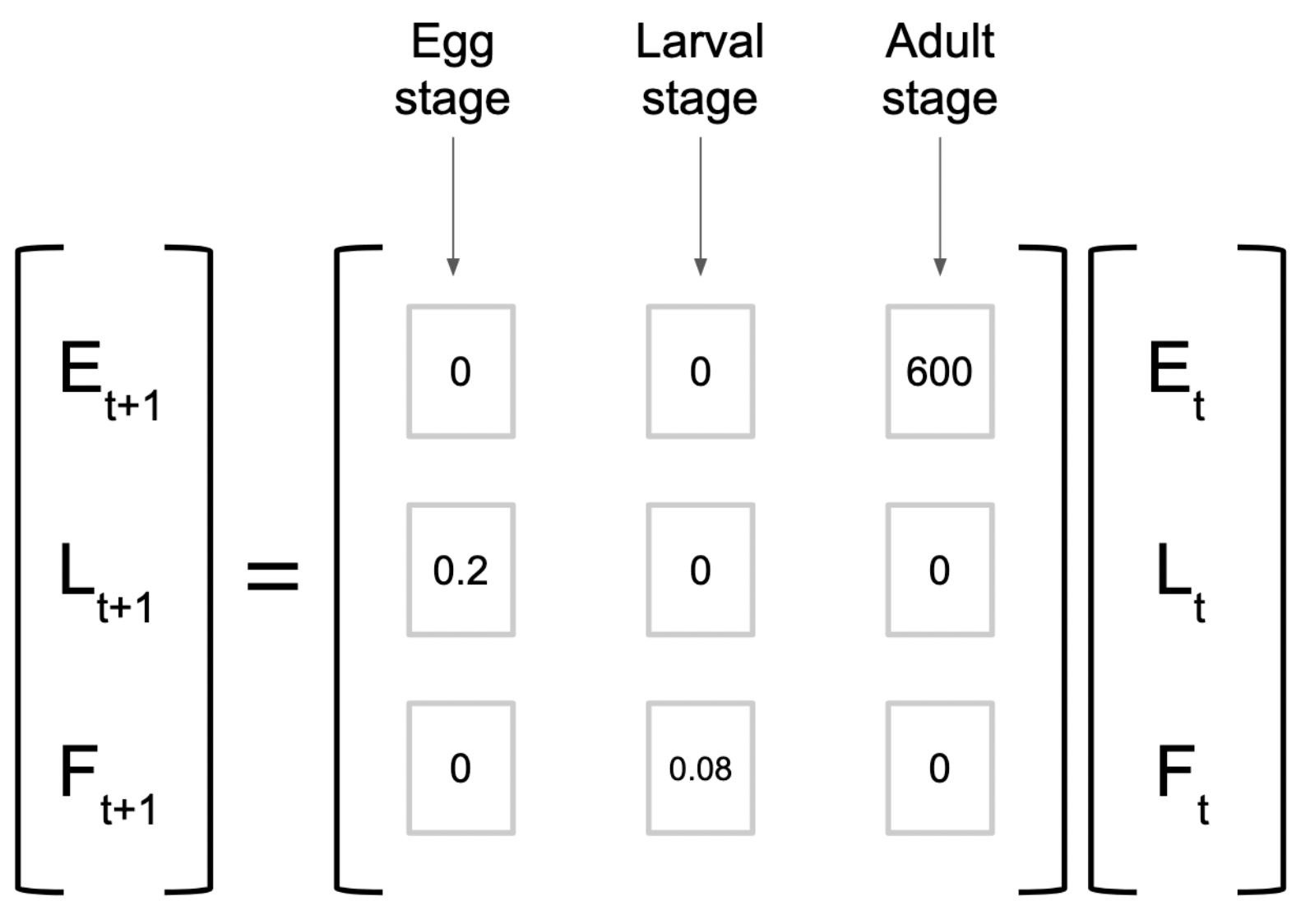
Let’s say we start with 12000 eggs, 700 larvae, and 500 female adults. Create a vector containing those initial values:

# Insect lifestage populations (year 0) ----
insect_y0 <- c(12000, 700, 500)

Find the populations for each life stage at t = 1 year

Reminder: this means we’ll take the dot product of our projection matrix, and the lifestage populations.

# Populations at year 1 ----
insect_y1 <- insect_leslie %*% insect_y0

# Check it out ----
insect_y1 
       [,1]
[1,] 300000
[2,]   2400
[3,]     56
You can verify the math by hand!

\[insects\;Y_2 = \begin{bmatrix} 0&0&600 \\ 0.2&0&0 \\ 0&0.08&0 \end{bmatrix} \times \begin{bmatrix} 1200 \\ 700 \\ 500 \end{bmatrix} = \begin{bmatrix} (0\times12000)+(0\times700)+(600\times500) \\ (0.2\times12000)+(0\times700)+(0\times500) \\ (0\times500)+(0.08\times700)+(0\times500) \end{bmatrix} = \begin{bmatrix} 300,000 \\ 2,400 \\ 56 \end{bmatrix}\]

# Populations by lifestage at year 2 ----
insect_y2 <- insect_leslie %*% insect_y1

# Check it out ----
insect_y2
      [,1]
[1,] 33600
[2,] 60000
[3,]   192
# Populations by lifestage at year 3 ---- 
insect_y3 <- insect_leslie %*% insect_y2

# Check it out ----
insect_y3
       [,1]
[1,] 115200
[2,]   6720
[3,]   4800
# Populations by lifestage at year 4: 
insect_y4 <- insect_leslie %*% insect_y3

# Check it out ----
insect_y4
          [,1]
[1,] 2880000.0
[2,]   23040.0
[3,]     537.6
Critical thinking: does it seem like there should be an easier way to do these repeated calculations?

Yes! Keep this in mind for EDS 221 when we start with iteration (for loops)!

4. Another Leslie matrix example

You have collected information about a type of tree. There are three life stages: seeds (S), juvenile (J) and adult (A). Juvenile trees don’t produce seeds. Adults produce 5000 seeds each year. 10% of seeds produced become seedlings (juveniles), and 6% of seedlings go on to become adults. 95% of adult trees survive each year.

  • Create the Leslie matrix for this population
  • Given an initial population structure of 5000 seeds, 0 juveniles, and 0 adults, project the population structure over 4 years.

It’s helpful to begin by drawing the Leslie matrix by hand:

\[\begin{bmatrix} S_{t+1} \\ J_{t+1} \\ A_{t+1} \end{bmatrix} = \begin{bmatrix} 0&0&5000 \\ 0.1&0&0 \\ 0&0.06&0.95 \end{bmatrix} \times \begin{bmatrix} S_t\\ J_t \\ A_t \end{bmatrix}\]

Where:

\[\begin{bmatrix} S_{t0}\\ J_{t0} \\ A_{t0} \end{bmatrix} = \begin{bmatrix} 5000\\ 0 \\ 0 \end{bmatrix}\]

# Make the projection matrix ----
tree_leslie <- matrix(c(0, 0, 5000, 0.10, 0, 0, 0, 0.06, 0.95), nrow = 3, ncol = 3, byrow = TRUE)

# Check it out (it should look just like the one you drew!) ----
tree_leslie
     [,1] [,2]    [,3]
[1,]  0.0 0.00 5000.00
[2,]  0.1 0.00    0.00
[3,]  0.0 0.06    0.95

Make some projections:

# year 0: initial condition ----
tree_0 <- c(5000, 0, 0)

# year 1 ----
tree_1 <- tree_leslie %*% tree_0
tree_1
     [,1]
[1,]    0
[2,]  500
[3,]    0
# year 2 ----
tree_2 <- tree_leslie %*% tree_1
tree_2
     [,1]
[1,]    0
[2,]    0
[3,]   30
# year 3 ----
tree_3 <- tree_leslie %*% tree_2
tree_3
         [,1]
[1,] 150000.0
[2,]      0.0
[3,]     28.5
# year 4 ----
tree_4 <- tree_leslie %*% tree_3
tree_4
           [,1]
[1,] 142500.000
[2,]  15000.000
[3,]     27.075

4. Send you modified files to GitHub!

You may choose to do so via the Git tab + buttons or via the RStudio Terminal.


End interactive session 4A