EDS 212: Day 2, Lecture 1

Definition of the derivative

---

August 6^th, 2024

Overview of Day 2 topics

---

• Derivatives
• Higher order & partial derivatives
• Differential equations (reading, understanding, solving, using)

What if we want to find an expression that describes the rate of change (slope) at any point on a function?

And that’s how we find derivatives

---

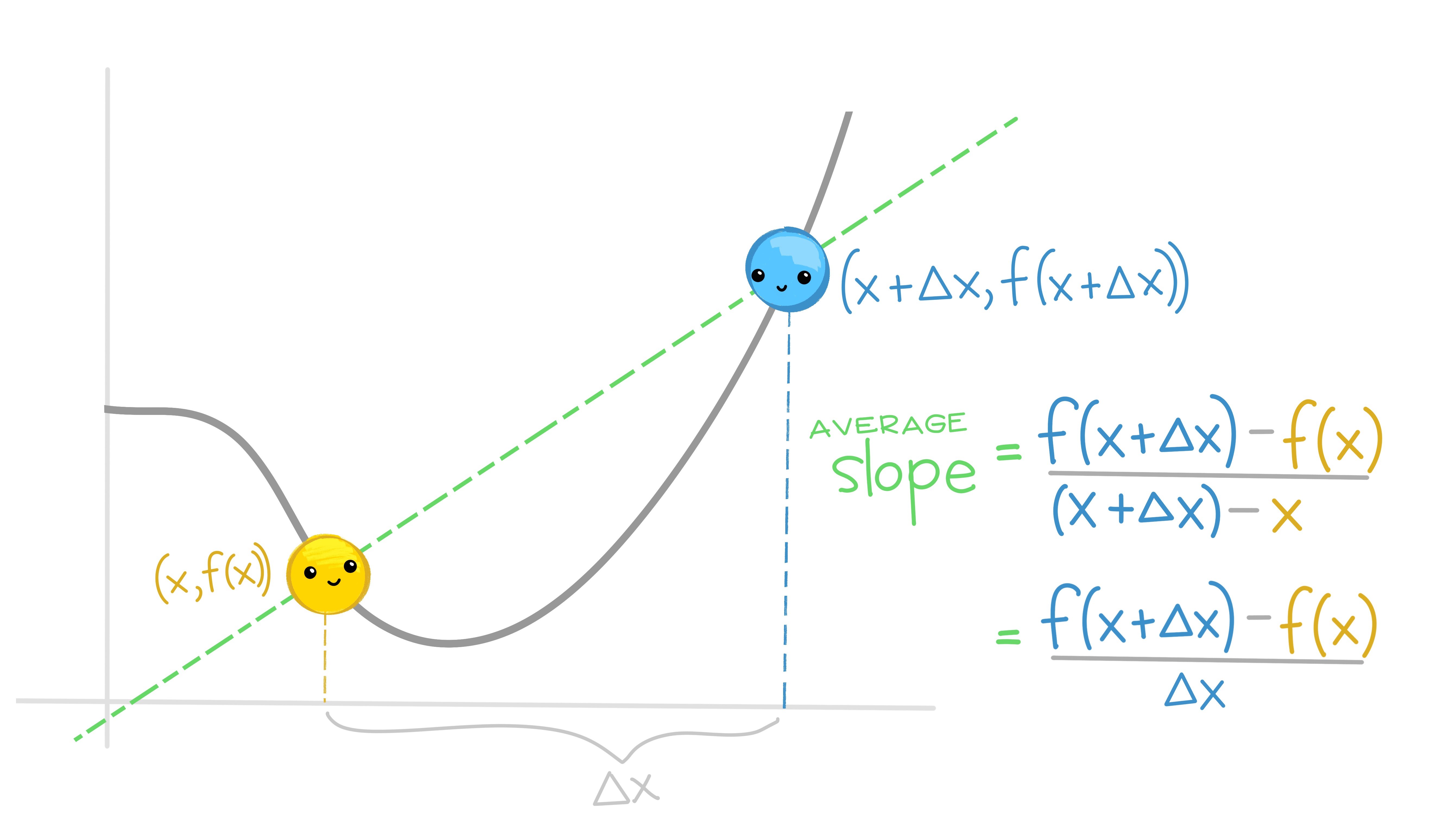
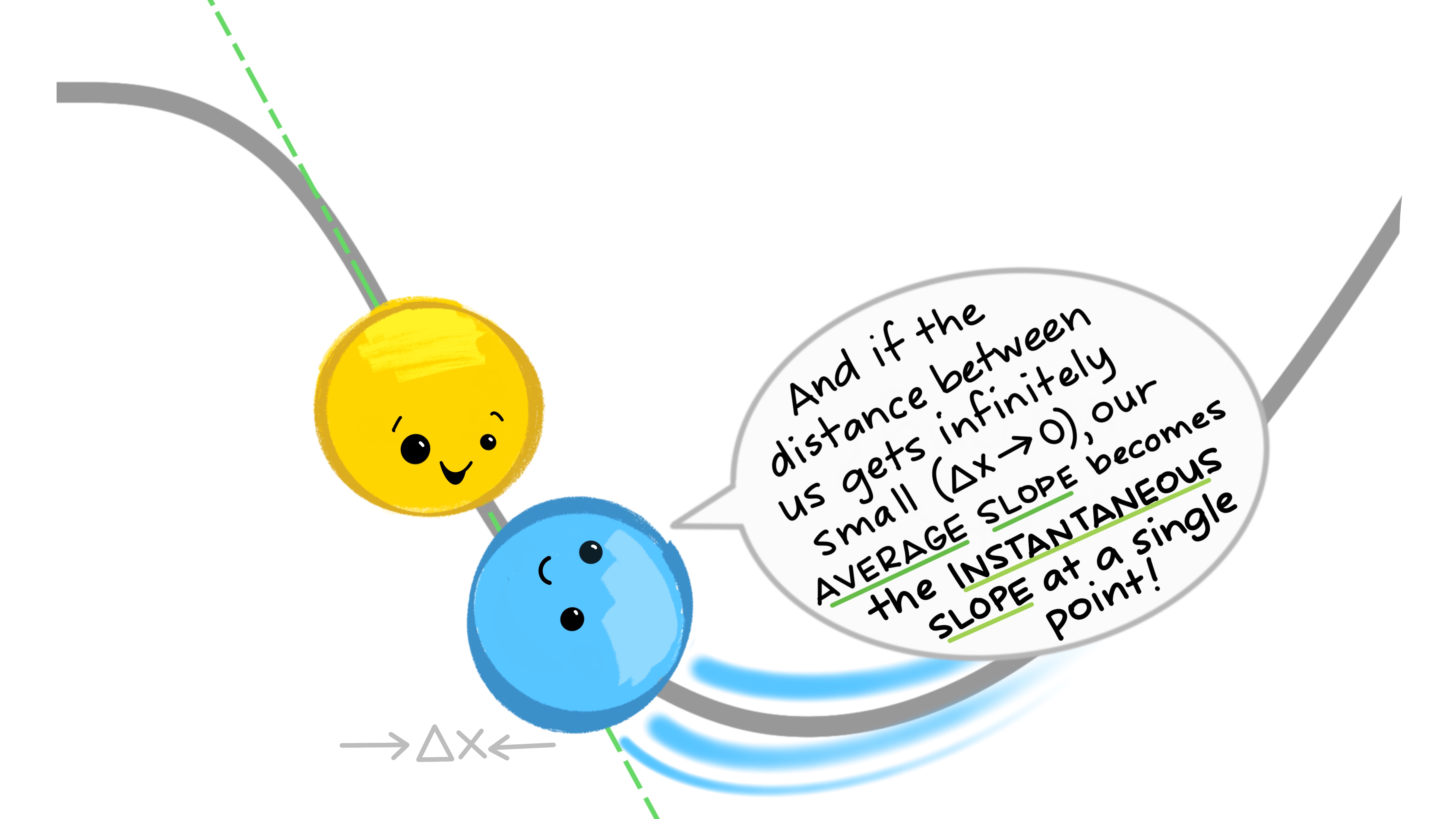
Evaluate the slope between two generic points on any function (separated by \(\Delta x\)) as \(\Delta x\) becomes infinitely small.

Let’s try one (NOTE we’re subbing \(h\) for \(\Delta x\))

---

Find an expression that tells us the slope of the function \(f(x)=x^2-18.2\) at any value of \(x\).

\[\frac{df}{dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]

\[=\lim_{h\to 0}\frac{((x+h)^2-18.2)-(x^2-18.2)}{h}\]

\[=\lim_{h\to 0}\frac{x^2+2xh+h^2-18.2-x^2+18.2}{h}\]

Which gets us to…

---

\[= \lim_{h\to 0} \frac{2xh+h^2}{h} = \lim_{h\to 0} {2x+h} = 2x\]

Your turn:

---

Find the derivative of the following using the definition of the derivative:

\[f(x)=4-x+3x^2\]

• \(= \lim_{h \to 0} \frac{df}{dx} = \frac{4 -(x+h) + 3 (x+h)^2 - (4-x+3x^2)}{h}\)
• \(= \lim_{h \to 0} \frac{df}{dx} = \frac{4 -(x+h) + 3 (x^2 + 2xh + h^2) - 4+x-3x^2)}{h}\)
• \(= \lim_{h \to 0} \frac{df}{dx} = \frac{4 -(x+h) + 3x^2 + 6xh + 3h^2 - 4+x-3x^2)}{h}\)
• \(= \lim_{h \to 0} \frac{df}{dx} = \frac{3h^2 + 6xh - h}{h}\)
• ANSWER: \(= \lim_{h \to 0} \frac{df}{dx} = 6x - 1\)

It’s cool to do that a few times, but it gets really tedious really fast.

---

So we have some basic derivative shortcut rules to speed it up a bit:

• Power rule: \(\frac{d}{dx}(x^n)=nx^{n-1}\)

• Constant rule: if \(k\) is a constant, \(\frac{d}{dx}(k)=0\)

• Constant multiple rule: if \(k\) is a constant, \(\frac{d}{dx}(kx) = k\space\)

• Sum and difference rule: \(\frac{d}{dx}(f(x)\pm g(x))=\frac{d}{dx} f(x)\pm \frac{d}{dx}g(x)\)

Yeah there are more - we’re not doing them.

ALL of those rules come from the definition of the derivative.

---

Reminder of what we’re doing mathematically:

---

Finding the slope between two generic points on a function as the distance between them gets infinitely small. That will give us an expression for the slope at any point on the original function.

Derivative of logs & exponents

---

• \(\frac{d}{dx}(e^x) = e^x\)

• \(\frac{d}{dx}ln(x)=\frac{1}{x}\)