EDS 212: Day 4, Lecture 1

Linear algebra continued

---

August 8^th, 2024

Part 1: Linear algebra continued

---

• Refresher: vectors and working with them
• Matrices: notation, language, basic algebra
• Representing systems of equations with matrices
• Linear algebra in environmental science

Matrices

---

A matrix is a table of values (multiple vectors in combination). A vector, therefore, can be thought of as a matrix with a single column.

• Dimensions: the size of the matrix, in rows x columns (m x n)
• Elements: values in a matrix, often denoted symbolically with a subscript where the first number is the row and the second number is the column (e.g. \(a_{34}\) indicates the element in row 3, column 4)

Matrix algebra (add / subtract)

---

Add or subtract the corresponding elements (by matrix position) to create a new matrix of the same dimensions.

Scalar multiplication

---

To multiply a matrix by a scalar, multiply each element in the matrix by the scalar to get a scaled matrix of the same dimensions.

For example:

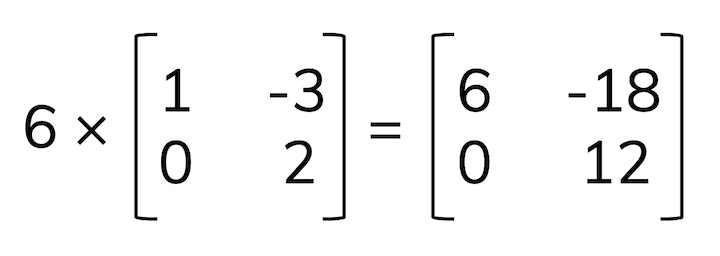
Recall: dot product

---

The dot product of two vectors is the sum of their elements multiplied:

For \(\vec a =[1,5]\) and \(\vec b = [2,-3]\):

\[\vec a \cdot \vec b=(1)(2)+(5)(-3)=-13\]

Matrix multiplication

---

We find the dot product of row \(\cdot\) column vectors:

Practice problems

---

(2)(1)+(-1)(6)…(2)(5)+(-1)(-3)

(0)(1)+(4)(6)…(0)(5)+(4)(-3)

\(solution = \begin{bmatrix} -4 & 13 \\ 24 & -12 \end{bmatrix}\)

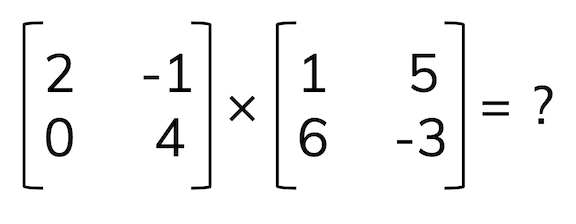
Critical thinking: Matrices with unequal dimensions

---

What do you think the output matrix would contain if you were multiplying the following?

The resulting matrix has dimensions which are equal to the number of the rows of the first matrix and the number of columns of the second matrix.

AG+BI+CK…AH+BJ+CL

DG+EI+FK…DH+EJ+FL

Let’s try one!

---

(0)(-1)+(2)(5)+(-1)(-3)…(0)(0)+(2)(1)+(-1)(6)

(3)(-1)+(4)(5)+(-2)(-3)…(3)(0)+(4)(1)+(-2)(6)

\(solution = \begin{bmatrix} 13 & -4 \\ 23 & -8 \end{bmatrix}\)

Diagonal matrix

---

A diagonal matrix is (almost always) a square matrix (\(m\) = \(n\)) where only elements on the diagonal are non-zero values.

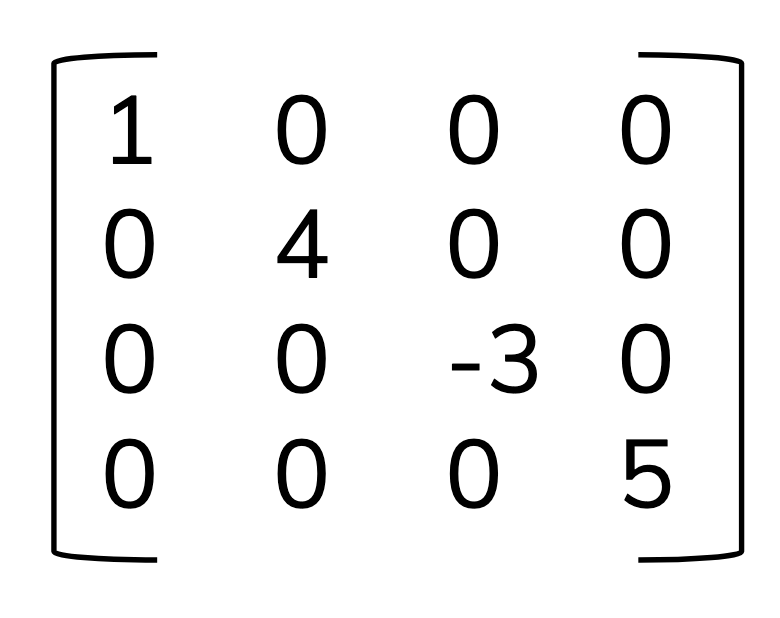
What happens when we multiply a matrix by a diagonal matrix?

---

A diagonal matrix is also called a scaling matrix because it scales rows proportionally, but not by the same value:

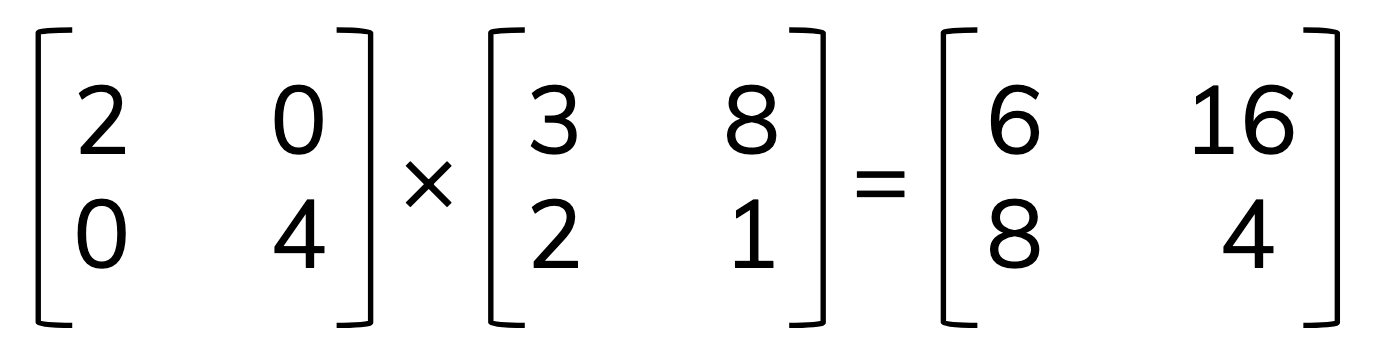
Matrices as systems of equations

---

Often in environmental data science, we have multiple equations representing processes. Matrices give us a way to express these systems of equations in data structures that are easy to store and work with in data science. For example, let’s say we have a system:

\[3x-8y=5\]

\[x + 2y = 10\]

How can we write this using matrices?

Rewriting in matrix form:

---

\[3x-8y=5\]

\[x + 2y = 10\]

The matrix form of this system of equations looks as follows:

We can write systems of equations in matrix form as \(Ax=b\), where:

• \(A\) is the coefficient matrix
• \(x\) is the vector of variables
• \(b\) is the constant vector

1. Identify coefficients to form matrix \(A\), where each row corresponds to the coefficients of one equation:

\[A = \begin{bmatrix} 3 & -8 \\ 1 & 2 \end{bmatrix}\]

2. Form the variable vector \(x\) which contains the variables of the system:

\[x = \begin{bmatrix} x \\ y \end{bmatrix}\]

3. Form the constant vector \(b\) \[b = \begin{bmatrix} 5 \\ 10 \end{bmatrix}\]

Example: matrices and linear algebra in environmental science

---

Leslie Matrix: Population ecology

A matrix model that accounts for survival / fecundity rates at different life stages for a species.

The Leslie matrix is one of the most well-known ways to describe the growth of populations (and their projected age distribution), in which a population is:

• closed to migration,
• growing in an unlimited environment,
• and where only one sex, usually the female, is considered.

Overview:

---

• Define life stages

• Estimate probability of survival / reproduction at different life stages to create a matrix over time

• Combine into a matrix that allows calculation at the next time step

Writing estimates as equations:

---

For our species, each adult female will lay ~600 eggs during each cycle (let’s say that’s a year). Which means that the eggs at time \(t+1\) can be estimated by the number of adult females * 600:

\[E_{t+1}=600 * F_t\]

Writing estimates as equations:

---

\[E_{t+1}=600 * F_t\]

We also estimate that 20% of eggs survive to reach larval stage:

\[L_{t+1} = 0.2*E_t\]

Writing estimates as equations:

---

\[E_{t+1}=600 * F_t\] \[L_{t+1} = 0.2*E_t\]

We also estimate that 8% of those that reach larval stage will survive to become reproducing female adults:

\[F_{t+1}=0.08*L_t\]

How can we write this in matrix form?

---

\[E_{t+1}=600 * F_t\]

\[L_{t+1} = 0.2*E_t\]

\[F_{t+1}=0.08*L_t\]

The Leslie matrix (L) will be a 3x3 matrix since we have three stages (Eggs, Larvae, Adults).

Each column represents an age class at time \(t\)

1. Fecundity (Top Row): The third element of the top row is 600 because adult females contribute to the number of eggs in the next generation.

2. Survival Rates (Sub-diagonal):

• The first element in the second row (0.2) represents the probability of an egg surviving to become a larva.
• The second element in the third row (0.08) represents the probability of a larva surviving to become an adult female.

How can we write this in matrix form?

---

\[E_{t+1}=600 * F_t\]

\[L_{t+1} = 0.2*E_t\]

\[F_{t+1}=0.08*L_t\]

Leslie matrix

---

Leslie matrix

---

• Each column is the age class at time \(t\) and each row is the age class at time \(t+1\)
• Each entry represents a transition, or change in the # of individuals, from one age class to the next
• Fertilities are always in the first row, and represent the contributions to newborns from reproduction
• Survival probabilities are always in the subdiagonal and represent transitions from one age class to the next
• All other entries are 0 because no other transitions are possible – individuals cannot remain in the same age class from one year to the next, nor can they skip or repeat age classes