EDS 212: Day 5, Lecture 1

Basic probability theory

August 9th, 2024

The Monty Hall problem


Monty Hall Problem, by Numberphile

Why refresh probability?

  • Hypothesis testing
  • Bayesian statistics
  • Decision making
  • Dangers

Probability





Definition: the likelihood that an event or outcome occurs. Typically, \(P = 0\) indicates no chance of an event or outcome happening, \(P=1\) indicates it happens with certainty.

Terminology


Event space: The collection of all possible unique outcomes of an experiment or scenario. Also called the sample space.


Event: A possible outcome (or combination of outcomes). The probability of event \(A\) occurring is written as \(P\{ A \}\).


The probability is the long term relative frequency of an event occurring, given all outcomes of the event space.

Law of large numbers


If you repeat an experiment independently a large number of times, the calculated statistic (e.g. mean, proportion ‘true’, etc.) will be close to the true (expected) parameter.


Example: Proportion “heads” over a long run of coin flips, with a fair coin.


Let’s sketch what it might look like…

Basic probability theory, notation, and diagrams


  • Intersection: Probability that outcomes co-occur. In other words, these are AND probability statements.


  • Union: Probability that at least one outcome in the event space happens (could be just one, or all). In other words, these are OR probability statements.


  • Complement: Probability that an outcome or set of outcomes does not occur

Intersection


Notation: \(P\{A\cap B\}\)


In words: The probability of A and B happening (where A and B are independent events)


Calculation: \(P\{A\cap B\} = P\{A\}*P\{B\}\)

Union


Notation: \(P\{A\cup B\}\)


In words: The probability of A or B happening (i.e., at least A or B happens, or both).


Calculation: \(P\{A\cup B\}=P\{A\}+P\{B\}-P\{A\cap B\}\)

Complement


Notation: \(P\{A'\}\)


In words: The probability of \(A\) NOT happening


Calculation: \(P\{A'\}=1-P\{A\}\)

Conditional probability


If events are not independent, one event having occurred can change the probability of another event occurring. For events \(A\) and \(B\), the probability of \(B\) given that \(A\) is know to occur is:


\(P\{B|A\}=\frac{P\{A \cap\ B\}}{P\{A\}}\)


A common question: Why doesn’t this just simplify to \(P\{B\}\) if the intersection is \(P\{A\}*P\{B\}\)?

Intuition check



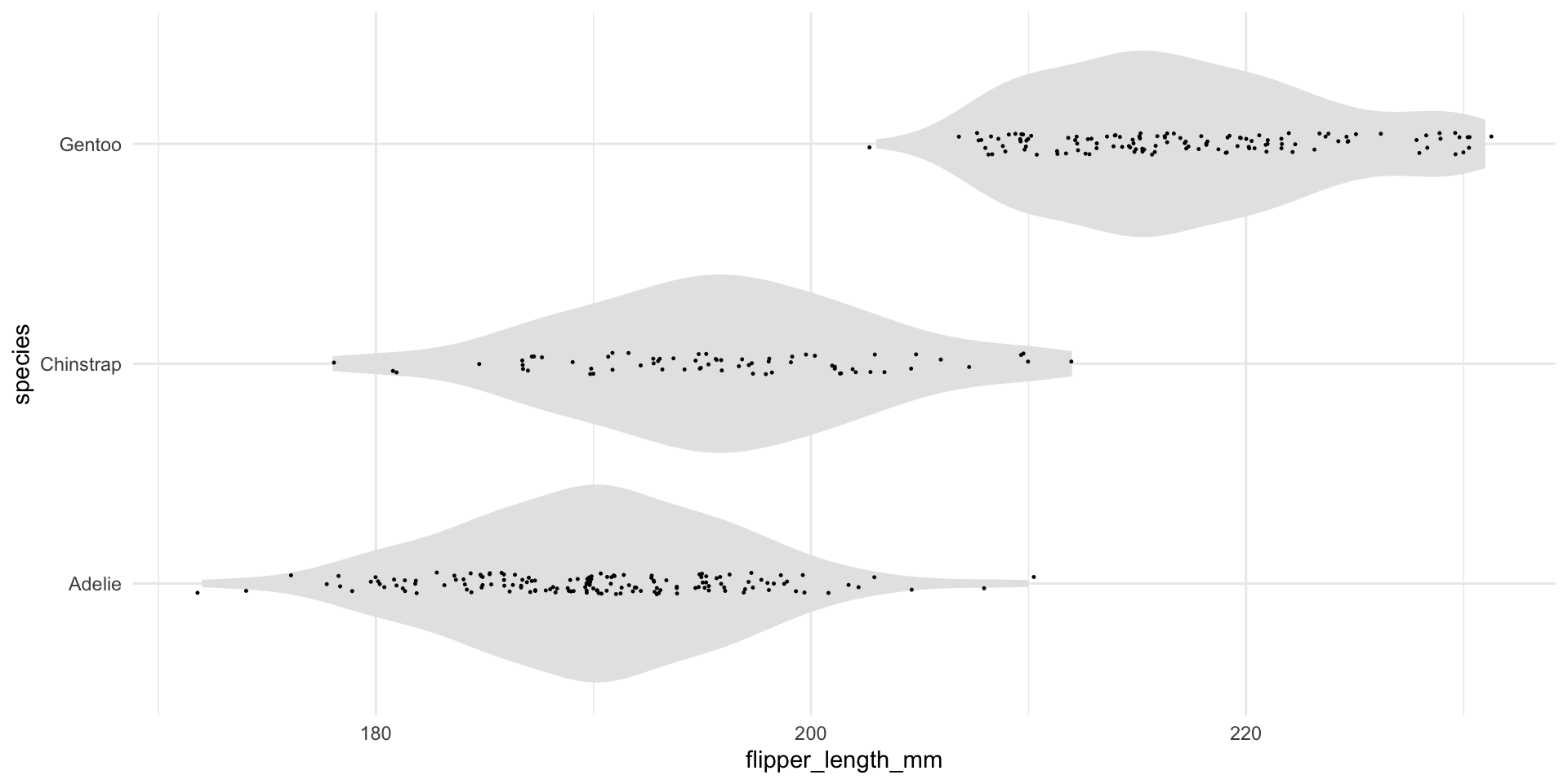
The following are jitterplots (overlaying violin plots) of flipper length for Adélie, Chinstrap and Gentoo penguins recorded by Dr. Kristen Gorman at islands in Palmer Archipelago, Antarctica.


We’ll consider: given some mystery penguins with different flipper lengths, how might the length inform which species we think it is?



Terms


  • Population: The entire collection of things in a category you are trying to understand. You define the population. For example: Santa Barbara registered voters, Ponderosa pines in Inyo National Forest, purple urchins in Channel Islands Marine Sanctuary.

  • Sample: A subset of the population, goal is to be representative of the population

  • Parameter: A characteristic of the population

  • Statistic: A characteristic of the sample

Inference




Usually, we don’t have the resources (time, money, human power, etc.) to collect observations for an entire population. As a proxy, we try to collect a representative sample.


Then, we attempt to draw conclusions about the populations from which our samples were collected.

Probability density function


On Day 4, we visualized data distributions from histograms. If we use histograms to estimate continuous functions that describe all possible outcomes, we have created a probability density function.


The area under any probability density function = 1, indicating that 100% of all possible outcomes are represented by the function.


Drawing fun!

This gives us a basis for hypothesis testing (EDS 222)


If a null hypothesis is true, what is the probability that your data outcome (e.g. mean, value, etc.) or something more extreme would have occurred by random chance?


Is that so unlikely (is the probability low enough), that you think you have sufficient evidence to reject the null hypothesis? Or not?


Let’s brainstorm some examples (and to be continued…)